In $\triangle \mathrm{ABC}$, points $\mathrm{P}$ and $\mathrm{Q}$ are on $\mathrm{CA}$ and $\mathrm{CB}$, respectively such that $\mathrm{CA}=16 \mathrm{~cm}, \mathrm{CP}=10 \mathrm{~cm}, \mathrm{CB}=30 \mathrm{~cm}$ and $\mathrm{CQ}=25 \mathrm{~cm}$. Is $\mathrm{PQ} \| \mathrm{AB}$ ?
Given: $A C=16 \mathrm{~cm}, C P=10 \mathrm{~cm}, C B=30 \mathrm{~cm}$ and $C Q=25 \mathrm{~cm}$, we get
We will check whether $\frac{C P}{A C}=\frac{C Q}{B C}$ or not to conclude whether $P Q \| A B$.
$\frac{C P}{A C}=\frac{10 \mathrm{~cm}}{16 \mathrm{~cm}}=\frac{5}{8}$
$\frac{C Q}{C B}=\frac{25 \mathrm{~cm}}{30 \mathrm{~cm}}=\frac{5}{6}$
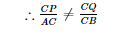
Hence, PQ is not parallel to AB.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
