In each of the figures [(i)-(iv)] given below,

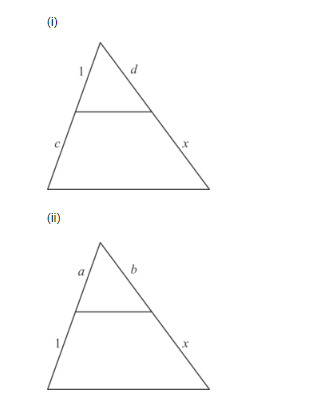
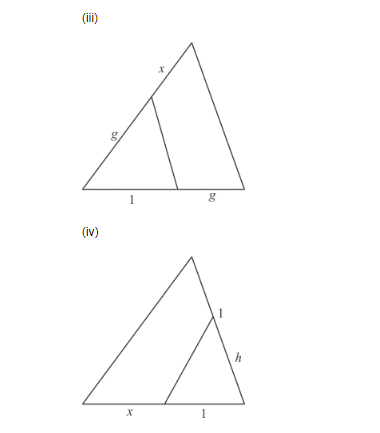
In each of the figure, we have to find the value of x

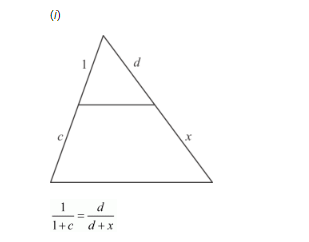
By cross multiplication on both sides, we get

$1 \times(d+x)=d \times(1+c)$

$d+x=d+d c$

$x=d+d c-d$

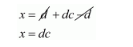
Hence the value of $x$ is $d c$.

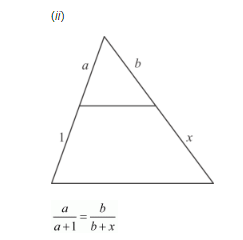
By cross multiplication on both sides, we get

$a \times(b+x)=b \times(a+1)$

$a b+a x=a b+b$

$a x=a b+h-a b$

$a x=a b+b-a b$

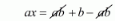
$a x=b$

$x=\frac{b}{a}$

Hence the value of $x$ is $\frac{b}{a}$.

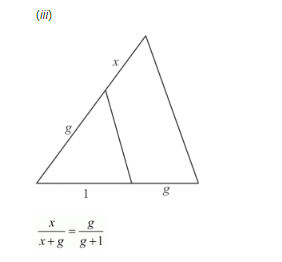
By cross multiplication on both sides, we get

$x \times(g+1)=g \times(x+g)$

$x g+x=g x+g^{2}$

$x=g x+g^{2}-g x$

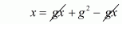
$x=g^{2}$

Hence the value of $x$ is $g^{2}$.

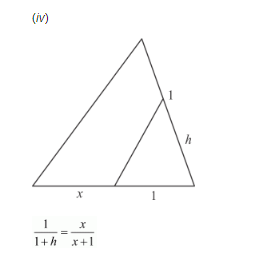
By cross multiplication on both sides, we get

$1 \times(x+1)=x \times(1+h)$

$x+1=x+h x$

$x+1-x=h x$

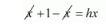
$1=x h$

$\frac{1}{h}=x$

Hence the value of $x$ is $\frac{1}{h}$.