In Figure, ABCD is a parallelogram in which ∠A = 60°. If the bisectors of ∠A, and ∠B meet at P, prove that AD = DP, PC = BC and DC = 2AD.
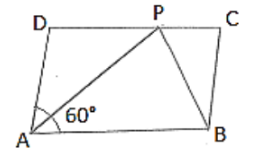
AP bisects ∠A
Then, ∠DAP = ∠PAB = 30°
Adjacent angles are supplementary
Then, ∠A + ∠B = 180°
∠B + 600 = 180°
∠B = 180° − 60°
∠B = 120°
BP bisects ∠B
Then, ∠PBA = ∠PBC = 30°
∠PAB = ∠APD = 30° [Alternate interior angles]
Therefore, AD = DP [Sides opposite to equal angles are in equal length]
Similarly
∠PBA = ∠BPC = 60° [Alternate interior angles]
Therefore, PC = BC
DC = DP + PC
DC = AD + BC [Since, DP = AD and PC = BC]
DC = 2AD [Since, AD = BC, opposite sides of a parallelogram are equal]
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
