Question:
In figure, if ∠OAB = 40°, then ∠ACB is equal to From Eq. (i) ∠ACB = ∠ADB = 70°
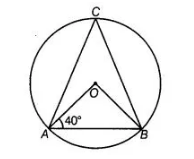
(a) 50°
(b) 40°
(c) 60°
(d) 70°
Solution:
(a)
In ΔQAB, OA = OB [both are the radius of a circle]
∠OAB = ∠OBA => ∠OBA = 40°
[angles opposite to equal sides are equal] Also, ∠AOB + ∠OBA + ∠BAO = 180°
[by angle sum property of a triangle]
∠AOB + 40° + 40° = 180°
=> ∠AOB = 180° – 80° = 100°
We know that, in a circle, the angle subtended by an arc at the centre is twice the angle subtended by it at the remaining part of the circle.
∠AOB = 2 ∠ACB => 100° =2 ∠ACB
∠ACB = 100°/2 = 50°
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
