In figure, O is the centre of the circle, BO is the bisector of ∠ABC. Show that AB = AC.

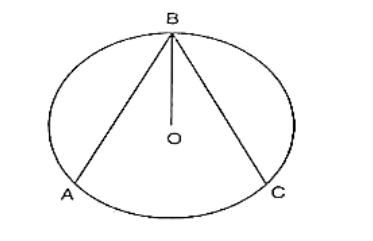
Given, BO is the bisector of ∠ABC

To prove AB = BC

Proof:

Since, BO is the bisector of ∠ABC.

Then, ∠ABO = ∠CBO ... (i)

Since, OB = OA         [Radius of circle]

Then, ∠ABO = ∠DAB... (ii)      [opposite angles to equal sides]

Since OB = OC                       [Radius of circle]

Then, ∠OAB = ∠OCB... (iii) [opposite angles to equal sides]

Compare equations (i), (ii) and (iii)

∠OAB = ∠OCB ... (iv)

In ΔOAB and ΔOCB

∠OAB = ∠OCB            From (iv)]

∠OBA = ∠OBC     [Given]

OB = OB                   [Common]

Then, ΔOAB ≅ ΔOCB [By AAS condition]

∴  AB = BC [CPCT]