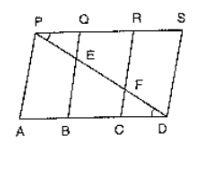
In figure, PSDA is a parallelogram in which PQ = QR = RS and AP ∥ BQ ∥ CR. Prove that ar (ΔPQE) = ar(ΔCFD).
Question:
In figure, PSDA is a parallelogram in which PQ = QR = RS and AP ∥ BQ ∥ CR. Prove that ar (ΔPQE) = ar(ΔCFD).
Solution:
Given that PSDA is a parallelogram
Since, AP ∥ BQ ∥ CR ∥ DS and AD ∥ PS
Therefore, PQ = CD (equ. 1)
In triangle BED, C is the midpoint of BD and CF ∥ BE
Therefore, F is the midpoint of ED
⇒ EF = PE
Similarly,
EF = PE
Therefore, PE = FD (equ. 2)
In triangles PQE and CFD, we have
PE = FD
Therefore, ∠ EPQ = ∠FDC [Alternate angles]
So, by SAS criterion, we have
ΔPQE ≅ ΔDCF
⇒ ar(ΔPQE) = ar(ΔDCF)