In the adjoining figure, OD is perpendicular to the chord AB of a circle with centre O.

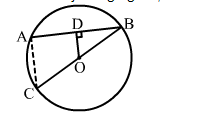
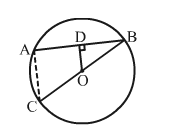
Given: BC is a diameter of a circle with centre O and OD ⊥ AB.
To prove: AC parallel to OD and AC = 2 × OD
Construction: Join AC.
Proof:
We know that the perpendicular from the centre of a circle to a chord bisects the chord.
Here, OD ⊥ AB
D is the mid point of AB.
i.e., AD = BD
Also, O is the mid point of BC.
i.e., OC = OB

Now, in ΔABC, we have:

D is the mid point of AB and O is the mid point of BC.
According to the mid point theorem, the line segment joining the mid points of any two sides of a triangle is parallel to the third side and equal to half of it.

i. e., $O D \| A C$ and $O D=\frac{1}{2} A C$

∴ AC = 2 × OD

Hence, proved.