Question:
In the figure, BA || ED and BC || EF. Show that ∠ABC = ∠DEF.
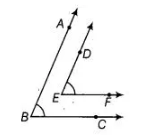
Solution:
Given BA || ED and BC || EF.
To show ∠ABC = ∠DEF.
Construction Draw a ray EP opposite to ray ED.
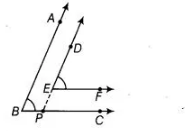
Proof In the figure, $B A \| E D$ or $B A \| D P$
$\therefore \quad \angle A B P=\angle E P C$ [corresponding angles]
$\Rightarrow \quad \angle A B C=\angle E P C$ $\ldots($ i)
Again, $B C \| E F$ or $P C \| E F$
$\therefore \quad \angle D E F=\angle E P C \quad$ [corresponding angles] ...(ii)
From Eqs. (i) and (ii),
$\angle A B C=\angle D E F$