In the following figure, ABCD is a rectangle,

Solution:

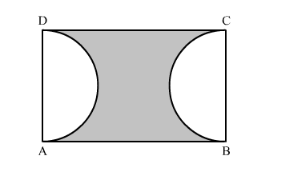
(i) We have given two semi-circles and a rectangle.

Area of the shaded region = Area of the rectangle − Area of the two semicircles ……..(1)

$\therefore$ Area of the shaded region $=20 \times 14-2 \times \frac{1}{2} \times \pi \times 7 \times 7$

Substituting $\pi=\frac{22}{7}$ we get,

$\therefore$ Area of the shaded region $=20 \times 14-2 \times \frac{1}{2} \times \frac{22}{7} \times 7 \times 7$

$\therefore$ Area of the shaded region $=20 \times 14-22 \times 7$

$\therefore$ Area of the shaded region $=280-154$

$\therefore$ Area of the shaded region $=126$

Therefore, area of shaded region is $126 \mathrm{~cm}^{2}$.

(ii) Now we will find length of the boundary of the shaded region.

$\therefore$ Length of the boundary the shaded region $=2 \pi r+A B+D C$

$\therefore$ Length of the boundary the shaded region $=2 \times \frac{22}{7} \times 7+20+20$

$\therefore$ Length of the boundary the shaded region $=2 \times 22+40$

$\therefore$ Length of the boundary the shaded region $=44+40$

 

$\therefore$ Length of the boundary the shaded region $=84$

Therefore, length of the boundary of the shaded region is $84 \mathrm{~cm}$.