Question:
In the given below figure rays OA, OB, OC, OP and OE have the common end point O. Show that ∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA = 360°
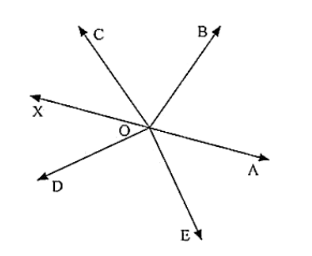
Solution:
Given that OA, OB, OD and OE have the common end point O.
A ray opposite to OA is drawn
Since ∠AOB, ∠BOF are linear pairs,
∠AOB + ∠BOF = 180°
∠AOB + ∠BOC + ∠COF = 180° .... (1)
Also,
∠AOE and ∠EOF are linear pairs
∠AOE + ∠EOF = 180°
∠AOE + ∠DOF + ∠DOE = 180° .... (2)
By adding (1) and (2) equations we get
∠AOB + ∠BOC + ∠COF + ∠AOE + ∠DOF + ∠DOE = 180°
∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA = 180°
Hence proved.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
