Question.
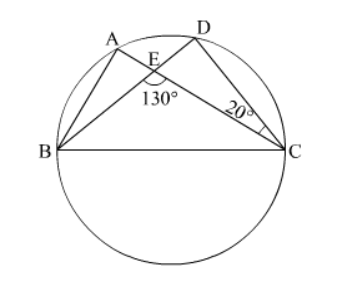
In the given figure, $A, B, C$ and $D$ are four points on a circle. $A C$ and $B D$ intersect at a point $E$ such that $\angle B E C=130^{\circ}$ and $\angle E C D=20^{\circ}$. Find $\angle B A C$.

Solution:
In $\triangle C D E$,
$\angle C D E+\angle D C E=\angle C E B$ (Exterior angle)
$\Rightarrow \angle C D E+20^{\circ}=130^{\circ}$
$\Rightarrow \angle C D E=110^{\circ}$
However, $\angle B A C=\angle C D E$ (Angles in the same segment of a circle)
$\Rightarrow \angle B A C=110^{\circ}$
In $\triangle C D E$,
$\angle C D E+\angle D C E=\angle C E B$ (Exterior angle)
$\Rightarrow \angle C D E+20^{\circ}=130^{\circ}$
$\Rightarrow \angle C D E=110^{\circ}$
However, $\angle B A C=\angle C D E$ (Angles in the same segment of a circle)
$\Rightarrow \angle B A C=110^{\circ}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
