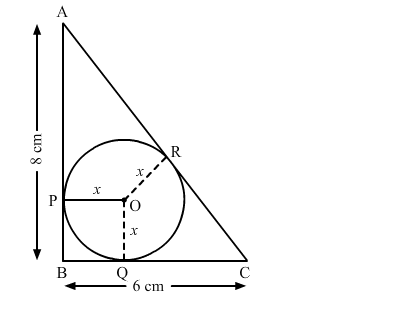
In the given figure, ΔABC is right-angled at B, such that BC = 6 cm and AB = 8 cm.

(a) 2 cm

Given, $A B=8 \mathrm{~cm}, B C=6 \mathrm{~cm}$

Now, in $\triangle A B C:$

$A C^{2}=A B^{2}+B C^{2}$

$\Rightarrow A C^{2}=\left(8^{2}+6^{2}\right)$

$\Rightarrow A C^{2}=(64+36)$

$\Rightarrow A C^{2}=100$

$\Rightarrow A C=\sqrt{100}$

$\Rightarrow A C=10 \mathrm{~cm}$

$P B Q O$ is a square.

$C R=C Q$ (Since the length $s$ of tangents drawn from an external point are equal)

$\therefore C Q=(B C-B Q)=(6-x) \mathrm{cm}$

Similarly, $A R=A P=(A B-B P)=(8-x) \mathrm{cm}$

$\therefore A C=(A R+C R)=[(8-x)+(6-x)] \mathrm{cm}$

$\Rightarrow 10=(14-2 x) \mathrm{cm}$

$\Rightarrow 2 x=4$

$\Rightarrow x=2 \mathrm{~cm}$

$\therefore$ The radius of the circle is $2 \mathrm{~cm}$.