In the given figure, from a rectangular region ABCD with AB

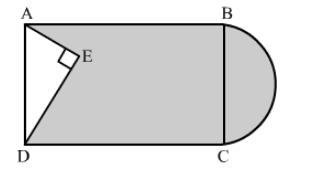
In right triangle AED
AD2 = AE2 + DE2  
= (9)2 + (12)2 
= 81 + 144
= 225
∴ AD2 = 225
⇒ AD = 15 cm
We know that the opposite sides of a rectangle are equal
AD = BC =  15 cm
= Area of the shaded region = Area of rectangle − Area of triangle  AED + Area of semicircle

$=\mathrm{AB} \times \mathrm{BC}-\frac{1}{2} \times \mathrm{AE} \times \mathrm{DE}+\frac{1}{2} \pi\left(\frac{\mathrm{BC}}{2}\right)^{2}$

$=20 \times 15-\frac{1}{2} \times 9 \times 12+\frac{1}{2} \times 3.14\left(\frac{15}{2}\right)^{2}$

$=300-54+88.31$

$=334.31 \mathrm{~cm}^{2}$

Hence, the area of shaded region is 334.31 cm2