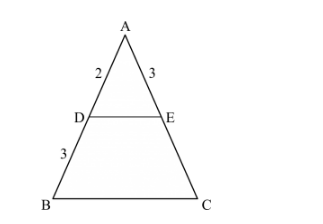
In the given figure, if ∠ADE = ∠ABC, then CE =

Given: $\angle \mathrm{ADE}=\angle \mathrm{ABC}$

To find: The value of CE

Since $\angle \mathrm{ADE}=\angle \mathrm{ABC}$

$\therefore \mathrm{DE} \| \mathrm{BC}$ (Two lines are parallel if the corresponding angles formed are equal)

According to basic proportionality theorem if a line is parallel to one side of a triangle intersecting the other two sides, then it divides the two sides in the same ratio.

In ∆ABC, DE || BC

$\frac{\mathrm{AD}}{\mathrm{DB}}=\frac{\mathrm{AE}}{\mathrm{EC}}$

$\frac{2}{3}=\frac{3}{E C}$

$\mathrm{EC}=\frac{3 \times 3}{2}$

$\mathrm{EC}=\frac{9}{2}$

Hence we got the result $(c)$.