In the given figure, if x = y and AB = CB, then prove that AE = CD.

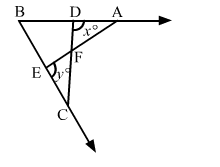
Solution:

Consider the triangles AEB and CDB.

$\angle E B A=\angle D B C$ (Common angle) ...(i)

Further, we have:

$\angle \mathrm{BEA}=180-\mathrm{y}$

$\angle \mathrm{BDC}=180-\mathrm{x}$

Since $\mathrm{x}=\mathrm{y}$, we have $:$

$180-\mathrm{x}=180-\mathrm{y}$

 

$\Rightarrow \angle \mathrm{BEA}=\angle \mathrm{BDC} \quad \ldots$ (ii)

$\mathrm{AB}=\mathrm{CB} \quad$ (Given) ...(iii)

From (i), (ii) and (iii), we have:

$\triangle B D C \cong \triangle B E A$ (AAS criterion)

$\therefore \mathrm{AE}=\mathrm{CD}(\mathrm{CPCT})$

 

Hence, proved.