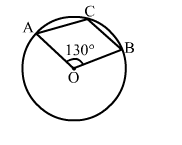
In the given figure, O is the centre of a circle and ∠AOB = 130°.

(c) 115°
Join AB.
Then chord AB subtends ∠AOB at the centre and ∠ADB at a point D of the remaining parts of a circle.

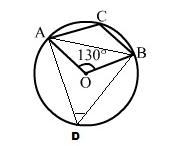
∴∠AOB = 2∠ADB

$\Rightarrow \angle \mathrm{ADB}=\frac{1}{2} \angle \mathrm{AOB}=\left(\frac{1}{2} \times 130^{\circ}\right)=65^{\circ}$

In cyclic quadrilateral, we have:
∠ADB + ∠ACB = 180°
⇒ 65° + ∠ACB = 180°
∴∠ACB = (180° - 65°) = 115°