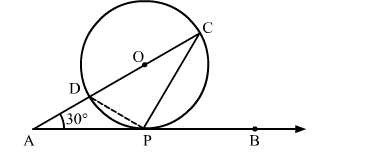
In the given figure, O is the centre of the circle. AB is the tangent to the circle at the point P.

We know that a chord passing through the centre is the diameter of the circle.
∵∠DPC = 90∘    (Angle in a semi circle is 90∘)
 Now, In △CDP
∠CDP + ∠DCP + ∠DPC = 180∘            [Angle sum property of a triangle]
⇒ ∠CDP + ∠DCP +  90∘ = 180∘                      
⇒ ∠CDP + ∠DCP = 90∘
By using alternate segment theorem
We have ∠CDP = ∠CPB
∴∠CPB + ∠ACP = 90∘
Hence, the correct answer is option (b).