In the given figure, PA and PB are tangents from an external point P to a circle with centre O. LN touches the circle at M. Prove that PL + LM = PN + MN.
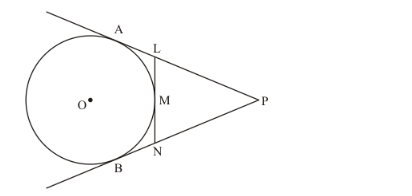
The figure given in the question
From the property of tangents we know that the length of two tangents drawn from an external point will we be equal. Hence we have,
PA = PB
PL + LA = PN + NB …… (1)
Again from the same property of tangents we have,
LA = LM (where L is the common external point for tangents LA and LM)
NB = MN (where N is the common external point for tangents NB and MN)
Substituting LM and MN in place of LA and NB in equation (1), we have
PL + LM = PN + MN
Thus we have proved.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
