K, L, M and N are points on the sides AB, BC, CD and DA respectively of a square

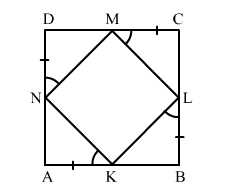
​Given: In square ABCD, AK = BL = CM = DN. 

To prove: KLMN is a square.
 
Proof:

In square ABCD,

AB = BC = CD = DA             (All sides of a square are equal.)

And, AK = BL = CM = DN     (Given)

So, AB -">−- AK = BC -">−- BL = CD -">−- CM = DA -">−- DN

⇒">⇒ KB = CL = DM = AN        ...(1)

In $\Delta N A K$ and $\Delta K B L$,

$\angle N A K=\angle K B L=90^{\circ}$ (Each angle of a square is a right angle.)

$A K=B L$                          (Given)

$A N=K B$                       [From (1)]

So, by SAS congruence criteria,

$\Delta N A K \cong \Delta K B L$

$\Rightarrow N K=K L \quad(\mathrm{CPCT}) \quad \ldots(2)$

Similarly,

$\Delta M D N \cong \Delta N A K$

$\Delta D N M \cong C M L$

$\Delta M C L \cong L B K$

$\Rightarrow M N=N K$ and $\angle D N M=\angle K N A \quad$ (CPCT) $\quad$...(3)

$M N=J M$ and $\angle D N M=\angle C M L \quad$ (CPCT) $\quad \ldots$ (4)

$M L=L K$ and $\angle C M L=\angle B L K \quad$ (CPCT) $\quad \ldots$ (5)

From (2), (3), (4) and (5), we get

NK = KL = MN = ML      ...(6)

And, $\angle D N M=\angle A K N=\angle K L B=L M C$

Now,

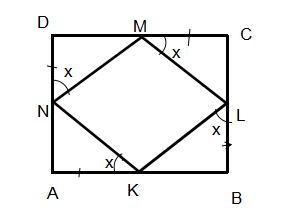
In $\Delta N A K$,

$\angle N A K=90^{\circ}$

Let $\angle A K N=x^{\circ}$

So, $\angle D N K=90^{\circ}+x^{\circ}$ (Exterior angles equals sum of interior opposite angles.)

$\Rightarrow \angle D N M+\angle M N K=90^{\circ}+x^{\circ}$

$\Rightarrow x^{\circ}+\angle M N K=90^{\circ}+x^{\circ}$

$\Rightarrow \angle M N K=90^{\circ}$

Similarly,

$\angle N K L=\angle K L M=\angle L M N=90^{\circ}$    (7)

Using (6) and (7), we get
 
All sides of quadrikateral KLMN are equal and all angles are 90°">°°.

So, KLMN is a square.