On a square handkerchief, nine circular designs each of radius 7 cm are made.

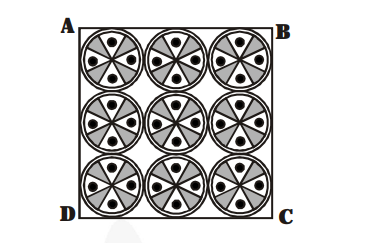
$\because$ The circles touch each other.

$\therefore$ The side of the square $A B C D$

= 3 × diameter of a circle

= 3 × (2 × radius of a circle) = 3 × (2 × 7 cm)

= 42 cm 

$\rightarrow$ Area of the sollare $A B(\mid)=42 \times 42 \mathrm{~cm}^{2}$

$=1764 \mathrm{~cm}^{2}$

Now, area of one circle $=\pi \mathrm{r}^{2}$

$\Rightarrow \frac{22}{7} \times 7 \times 7 \mathrm{~cm}^{2}=154 \mathrm{~cm}^{2}$

$\because$ There are 9 circles

$\therefore$ Total area of 9 circles $=154 \times 9=1386 \mathrm{~cm}^{2}$

$\therefore$ Area of the remaining portion of the handkerchief

$=(1764-1386) \mathrm{cm}^{2}=378 \mathrm{~cm}^{2} .$