Question:
On dividing, $3 x^{3}+x^{2}+2 x+5$ by a polynomial $g(x)$, the quotient and remainder are $3 x-5$ and $9 x+10$ respectively. Find $g(x)$
Solution:
By using division rule, we have
Divided = Quotient × Divisor + Remainder
$\therefore 3 x^{3}+x^{2}+2 x+5=(3 x-5) g(x)+9 x+10$
$\Rightarrow 3 x^{3}+x^{2}+2 x+5-9 x-10=(3 x-5) g(x)$
$\Rightarrow 3 x^{3}+x^{2}-7 x-5=(3 x-5) g(x)$
$\Rightarrow g(x)=\frac{3 x^{3}+x^{2}-7 x-5}{3 x-5}$
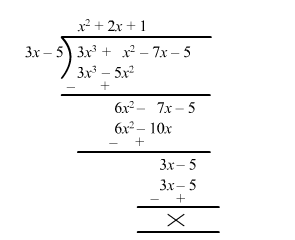
$\therefore g(x)=x^{2}+2 x+1$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
