P, Q, R and S are respectively the mid-points of the sides AB, BC, CD and DA of a quadrilateral ABCD in which AC = BD. Prove that PQRS is a
rhombus,
Thinking Process
Firstly, use the mid-point theorem in various triangles of a quadrilateral. Further show that the line segments formed by joining the mid-points are
equal, which prove the required quadrilateral.
Given In a quadrilateral ABCD, P, Q, R and S are the mid-points of sides AB, BC, CD and DA, respectively. Also, AC = BD To prove PQRS is a
rhombus.
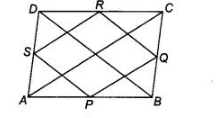
Proof In $\triangle A D C, S$ and $R$ are the mid-points of $A D$ and $D C$ respectively. Then, by mid-point theorem.
$S R \| A C$ and $S R=\frac{1}{2} A C$ $\ldots(1)$
In $\triangle A B C, P$ and $Q$ are the mid-points of $A B$ and $B C$ respectively. Then, by mid-point theorem
$P Q \| A C$ and $P Q=\frac{1}{2} A C$ $\ldots$ (ii)
From Eqs. (i) and (ii), $S R=P Q=\frac{1}{2} A C$ ....(iii)
Similarly, in $\triangle B C D$, $S P \| B D$ and $S P=\frac{1}{2} B D$.....(iv)
And in $\triangle B A D$, $S P \| B D$ and $S P=\frac{1}{2} B D$ ...(v)
From Eqs. (iv) and (v). $S P=R Q=\frac{1}{2} B D=\frac{1}{2} A C$ [given, $A C=B D] \ldots$ (vi)
From Eqs. (iii) and (vi), $\quad S R=P Q=S P=R Q$
It shows that all sides of a quadrilateral $P Q R S$ are equal. Hence, $P Q R S$ is a rhombus.
Hence proved.