Places A and B are 100 km apart on a highway. One car starts from A and another from B at the same time.

Let x and y be two cars starting from points A and B respectively.

Let the speed of the car X be x km/hr and that of the car Y be y km/hr.

Case I: When two cars move in the same directions:

Suppose two cars meet at point Q, then,

Distance travelled by car X=AQ

Distance travelled by car Y=BQ

It is given that two cars meet in 5 hours.

Distance travelled by car $X$ in 5 hours $=5 x \mathrm{~km} \mathrm{AQ}=5 x$

Distance travelled by car $Y$ in 5 hours $=5 y \mathrm{~km} \mathrm{BQ}=5 y$

Clearly $\mathrm{AQ}-\mathrm{BQ}=\mathrm{AB} 5 x-5 y=100$

Both sides divided by 5, we get $x-y=20 \cdots(i)$

Case II: When two cars move in opposite direction

Suppose two cars meet at point P, then,

Distance travelled by X car X=AP

Distance travelled by Y car Y=BP

In this case, two cars meet in 1 hour

Therefore, 

Distance travelled by car $y$ in 1 hours $=1 x \mathrm{~km}$

Distance travelled by car $y$ in 1 hours $=1 y \mathrm{~km}$

$A P+B P=A B$

$1 x+1 y=100$

$x+y=100$

$x+y=100$....(3)

By solving (i) and (ii) we get,

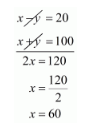
By substituting $x=60$ in equation (ii), we get

$x+y=100$

$60+y=100$

$y=100-60$

$y=40$

Hence, speed of car $X$ is $60 \mathrm{~km} / \mathrm{hr}$, speed of car $Y$ is $40 \mathrm{~km} / \mathrm{hr}$.