Prove that the lines joining the middle points of the opposite sides of a quadrilateral

Let us consider a Cartesian plane having a parallelogram OABC in which O is the origin.

We have to prove that middle point of the opposite sides of a quadrilateral and the join of the mid-points of its diagonals meet in a point and bisect each other.

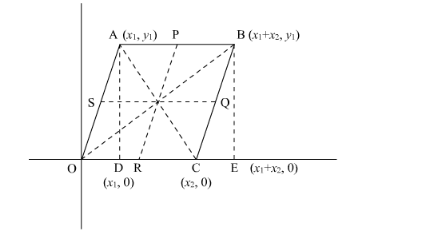
Let the co-ordinate of $\mathrm{A}$ be $\left(x_{1}, y_{1}\right)$. So the coordinates of other vertices of the quadrilateral are- $\mathrm{O}(0,0) ; \mathrm{B}\left(x_{1}+x_{2}, y_{1}\right) ; \mathrm{C}\left(x_{2}, 0\right)$

Let P, Q, R and S be the mid-points of the sides AB, BC, CD, DA respectively.

In general to find the mid-point $\mathrm{P}(x, y)$ of two points $\mathrm{A}\left(x_{1}, y_{1}\right)$ and $\mathrm{B}\left(x_{2}, y_{2}\right)$ we use section formula as,

$\mathrm{P}(x, y)=\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}+y_{2}}{2}\right)$

So co-ordinate of point P,

$=\left(\frac{x_{1}+x_{2}+x_{1}}{2}, \frac{y_{1}+y_{1}}{2}\right)$

$=\left(\frac{2 x_{1}+x_{2}}{2}, y_{1}\right)$

Similarly co-ordinate of point Q,

$=\left(\frac{x_{1}+x_{2}+x_{2}}{2}, \frac{y_{1}}{2}\right)$

$=\left(\frac{2 x_{2}+x_{1}}{2}, \frac{y_{1}}{2}\right)$

Similarly co-ordinate of point R,

$=\left(\frac{x_{2}}{2}, 0\right)$

Similarly co-ordinate of point S,

$=\left(\frac{x_{1}}{2}, \frac{y_{1}}{2}\right)$

Let us find the co-ordinates of mid-point of PR as,

$=\left(\frac{\frac{2 x_{1}+x_{2}}{2}+\frac{x_{2}}{2}}{2}, \frac{y_{1}}{2}\right)$

$=\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}}{2}\right)$

Similarly co-ordinates of mid-point of QS as,

$=\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}}{2}\right)$

Now the mid-point of diagonal AC,

$=\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}}{2}\right)$

Similarly the mid−point of diagonal OA,

$=\left(\frac{x_{1}+x_{2}}{2}, \frac{y_{1}}{2}\right)$

Hence the mid-points of PR, QS, AC and OA coincide.

Thus, middle point of the opposite sides of a quadrilateral and the join of the mid-points of its diagonals meet in a point and bisect each other.