Prove that the perimeter of a triangle is greater than the sum of its altitudes.

Solution:

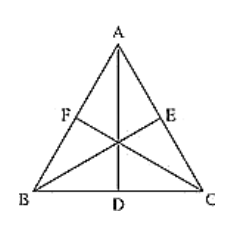
Given, ΔABC in which AD ⊥ BC, BE ⊥ AC and CF ⊥ AB.

To prove,

AD + BE + CF < AB + BC + AC

Figure:

Proof:

We know that of all the segments that can be drawn to a given line, from a point not lying on it, the perpendicular distance i.e, the perpendicular line segment is the shortest.

Therefore

AD ⊥ BC

AB > AD and AC > AD

AB + AC > 2AD .... (i)

BE ⊥ AC

BA > BE and BC > BE

BA + BC > 2BE ... (ii)

CF ⊥ AB

CA > CF and CB > CF

CA + CB > 2CF ... (iii)

Adding (i), (ii) and (iii), we get

AB + AC + BA + BC + CA + CB > 2AD + 2BE + 2CF

2AB + 2BC + 2CA > 2(AD + BE + CF)

AB + BC + CA > AD + BE + CF

The perimeter of the triangle is greater than that the sum of its altitudes

Hence proved