Prove that the volume of the largest cone that can be inscribed in a sphere of radius

Let r and h be the radius and height of the cone respectively inscribed in a sphere of radius R.

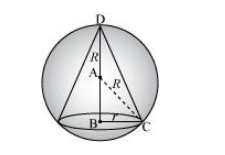
Let $V$ be the volume of the cone.

Then, $V=\frac{1}{3} \pi r^{2} h$

Height of the cone is given by,

$h=R+\mathrm{AB}=R+\sqrt{R^{2}-r^{2}} \quad[\mathrm{ABC}$ is a right triangle $]$

$\begin{aligned} \therefore V &=\frac{1}{3} \pi r^{2}\left(R+\sqrt{R^{2}-r^{2}}\right) \\ &=\frac{1}{3} \pi r^{2} R+\frac{1}{3} \pi r^{2} \sqrt{R^{2}-r^{2}} \end{aligned}$

$\therefore \frac{d V}{d r}=\frac{2}{3} \pi r R+\frac{2}{3} \pi r \sqrt{R^{2}-r^{2}}+\frac{1}{3} \pi r^{2} \cdot \frac{(-2 r)}{2 \sqrt{R^{2}-r^{2}}}$

$=\frac{2}{3} \pi r R+\frac{2}{3} \pi r \sqrt{R^{2}-r^{2}}-\frac{1}{3} \pi \frac{r^{3}}{\sqrt{R^{2}-r^{2}}}$

$=\frac{2}{3} \pi r R+\frac{2 \pi r\left(R^{2}-r^{2}\right)-\pi r^{3}}{3 \sqrt{R^{2}-r^{2}}}$

$=\frac{2}{3} \pi r R+\frac{2 \pi r R^{2}-3 \pi r^{3}}{3 \sqrt{R^{2}-r^{2}}}$

$\begin{aligned} \frac{d^{2} V}{d r^{2}} &=\frac{2 \pi R}{3}+\frac{3 \sqrt{R^{2}-r^{2}}\left(2 \pi R^{2}-9 \pi r^{2}\right)-\left(2 \pi r R^{2}-3 \pi r^{3}\right) \cdot \frac{(-2 r)}{6 \sqrt{R^{2}-r^{2}}}}{9\left(R^{2}-r^{2}\right)} \\ &=\frac{2}{3} \pi R+\frac{9\left(R^{2}-r^{2}\right)\left(2 \pi R^{2}-9 \pi r^{2}\right)+2 \pi r^{2} R^{2}+3 \pi r^{4}}{27\left(R^{2}-r^{2}\right)^{\frac{3}{2}}} \end{aligned}$

Now, $\frac{d V}{d r}=0 \Rightarrow \frac{2}{3} r R=\frac{3 \pi r^{3}-2 \pi r R^{2}}{3 \sqrt{R^{2}-r^{2}}}$

$\Rightarrow 2 R=\frac{3 r^{2}-2 R^{2}}{\sqrt{R^{2}-r^{2}}} \Rightarrow 2 R \sqrt{R^{2}-r^{2}}=3 r^{2}-2 R^{2}$

$\Rightarrow 4 R^{2}\left(R^{2}-r^{2}\right)=\left(3 r^{2}-2 R^{2}\right)^{2}$

$\Rightarrow 4 R^{4}-4 R^{2} r^{2}=9 r^{4}+4 R^{4}-12 r^{2} R^{2}$

$\Rightarrow 9 r^{4}=8 R^{2} r^{2}$

$\Rightarrow r^{2}=\frac{8}{9} R^{2}$

When $r^{2}=\frac{8}{9} R^{2}$, then $\frac{d^{2} V}{d r^{2}}<0$

$\therefore$ By second derivative test, the volume of the cone is the maximum when $r^{2}=\frac{8}{9} R^{2}$.

When $r^{2}=\frac{8}{9} R^{2}, h=R+\sqrt{R^{2}-\frac{8}{9} R^{2}}=R+\sqrt{\frac{1}{9} R^{2}}=R+\frac{R}{3}=\frac{4}{3} R$.

Therefore,

$=\frac{1}{3} \pi\left(\frac{8}{9} R^{2}\right)\left(\frac{4}{3} R\right)$

$=\frac{8}{27}\left(\frac{4}{3} \pi R^{3}\right)$

$=\frac{8}{27} \times($ Volume of the sphere $)$

Hence, the volume of the largest cone that can be inscribed in the sphere is $\frac{8}{27}$

the volume of the sphere.