Show that

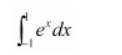
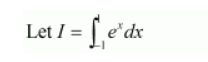  ...(1)

It is known that,

$\int_{a}^{b} f(x) d x=(b-a) \lim _{n \rightarrow \infty} \frac{1}{n}[f(a)+f(a+h) \ldots f(a+(n-1) h)]$, where $h=\frac{b-a}{n}$

Here, $a=-1, b=1$, and $f(x)=e^{x}$

$\therefore h=\frac{1+1}{n}=\frac{2}{n}$

$\therefore I=(1+1) \lim _{n \rightarrow \infty} \frac{1}{n}\left[f(-1)+f\left(-1+\frac{2}{n}\right)+f\left(-1+2 \cdot \frac{2}{n}\right)+\ldots+f\left(-1+\frac{(n-1) 2}{n}\right)\right]$

$=2 \lim _{n \rightarrow \infty} \frac{1}{n}\left[e^{-1}+e^{\left(-1+\frac{2}{n}\right)}+e^{\left(-1+2 \frac{2}{n}\right)}+\ldots e^{\left(-1+(n-1) \frac{2}{n}\right)}\right]$

$=2 \lim _{n \rightarrow \infty} \frac{1}{n}\left[e^{-1}\left\{1+e^{\frac{2}{n}}+e^{\frac{4}{n}}+e^{\frac{6}{n}}+e^{(n-1)^{2}} \frac{2}{n}\right\}\right]$

$=2 \lim _{n \rightarrow \infty} \frac{e^{-1}}{n}\left[\frac{e^{\frac{2 n}{n}-1}}{e^{\frac{2}{n}-1}}\right]$

$=e^{-1} \times 2 \lim _{n \rightarrow \infty} \frac{1}{n}\left[\frac{e^{2}-1}{e^{\frac{2}{n}-1}}\right]$

$=\frac{e^{-1} \times 2\left(e^{2}-1\right)}{\lim _{\frac{2}{n} \rightarrow 0}\left(\frac{e^{\frac{2}{n}}-1}{\frac{2}{n}}\right) \times 2}$

$=e^{-1}\left[\frac{2\left(e^{2}-1\right)}{2}\right]$            $\left[\lim _{h \rightarrow 0}\left(\frac{e^{h}-1}{h}\right)=1\right]$

$=\frac{e^{2}-1}{e}$

$=\left(e-\frac{1}{e}\right)$