Question:
A particle is projected with a speed $u$ at an angle 0 with the horizontal. Consider a small part of its path near the highest position and take it approximately to be a circular arc. What is the radius of this circle? This radius is called the radius of curvature of the curve at the point.
Solution:
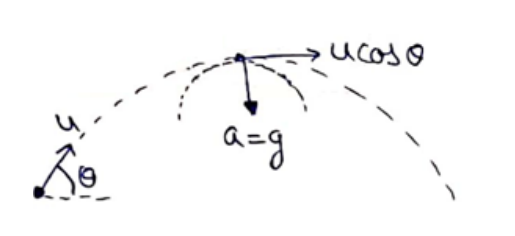
At highest point
$\mathrm{A}_{\text {radial }}=\frac{v 2}{R}$
$g=\frac{(u \cos \theta)^{2}}{R}$
$R=\frac{u^{2} \cos ^{2} \theta}{g}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
