Consider the situation of the previous problem. The man has to reach the other shore at the point directly opposite to his starting point. If he reaches the other shore somewhere else, he has to walk down to this point, Find the minimum distance that he has to walk.
When $\mathrm{V}_{\text {river }}>\mathrm{v}_{\text {manand }}$ for minimum drift $\sin \theta=\frac{\mathrm{V}_{\text {Man }}}{\mathrm{V}_{\text {river }}}$
$\sin \theta=\frac{3}{5}$
$\theta=37^{\circ}$
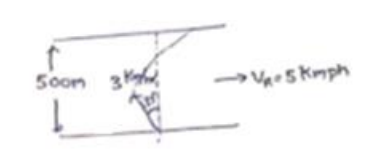
Time to cross river= $\frac{\text { distance }}{\text { speed }}$
$=\frac{0.5}{=3 \cos 37}$
drift=speed $\times$ time
$=\left(5-3 \sin 37^{\circ}\right)$ time
$=\left(5-3 \sin 37^{\circ}\right)$ time
$=\left(5-d^{\times \frac{3}{5}}\right)\left(\frac{0.5 \times 5}{12}\right)$
drift= $=\frac{2}{3} \mathrm{~km}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
