Question:
Solve the following system of inequalities graphically: 2x – y > 1, x – 2y < –1
Solution:
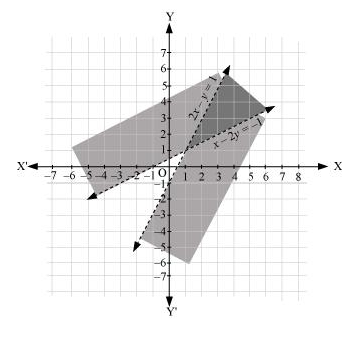
$2 x-y>1 \ldots(1)$
$x-2 y<-1 \ldots(2)$
The graph of the lines, $2 x-y=1$ and $x-2 y=-1$, are drawn in the figure below.
Inequality (1) represents the region below the line, $2 x-y=1$ (excluding the line $2 x-y=1$ ), and inequality (2) represents the region above the line, $x-2 y=-1$ (excluding the line $x-2 y=-1$ ).
Hence, the solution of the given system of linear inequalities is represented by the common shaded region excluding the points on the respective lines as follows.
