Solve the following systems of equations:

The given equations are:

$\frac{2}{x}+\frac{3}{y}=\frac{9}{x y} \quad \ldots(i)$

$\frac{4}{x}+\frac{9}{y}=\frac{21}{x y} \ldots($ ii $)$

Multiply equation (i) by 3 and subtract (ii) from (i), we get

$\frac{6}{x}+\frac{9}{y}=\frac{27}{x y}$

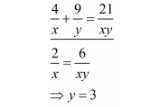
Put the value of $x$ in equation $(i)$, we get

$\Rightarrow \frac{2}{x}+\frac{3}{3}=\frac{9}{3 x}$

$\Rightarrow \frac{1}{x}=1$

$\Rightarrow x=1$

Hence the value of $x=1$ and $y=3$