Question:
The area (in sq. units) of the region $A=\{(x, y):(x-1)[x] \leq y \leq 2 \sqrt{x}, 0 \leq x \leq 2\}$, where $[t]$ denotes the greatest integer function, is :
Correct Option:
Solution:
$[x]=0$ when $x \in[0,1)$ and $[x]=1$ when $x \in[1,2)$
$y=\left\{\begin{array}{cc}0 & 0 \leq x<1 \\ x-1 & 1 \leq x<2\end{array}\right.$
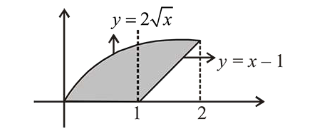
$\therefore A=\int_{0}^{2} 2 \sqrt{x} d x-\frac{1}{2}(1)(1)$
$=\left.\frac{4 x^{3 / 2}}{3}\right|_{0} ^{2}-\frac{1}{2}=\frac{8 \sqrt{2}}{3}-\frac{1}{2}$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
