The circumference of a circle is 100 m. The side of a square inscribed in the circle is
(a) $50 \sqrt{2}$
(b) $\frac{50}{\pi}$
(c) $\frac{50 \sqrt{2}}{\pi}$
(d) $\frac{100 \sqrt{2}}{\pi}$
We have given the circumference of the circle that is 100 cm. If d is the diameter of the circle, then its circumference will be
.
$\therefore \pi d=100$
$\therefore d=\frac{100}{\pi}$
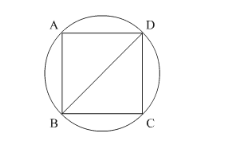
We obtained diameter of the circle. Look at the figure, diameter of the circle is also the diagonal of the square ABCD.
We know that if we have diagonal of the circle we can calculate the side of the square, using the formula given below,
Side $=\sqrt{2} \times$ diagonal
Substituting the value of diagonal we get,
Side $=\sqrt{2} \times \frac{100}{\pi}$
Therefore, side of the inscribed square is $\frac{100 \sqrt{2}}{\pi} \mathrm{cm}$.
Hence, the correct answer is option (d).