Question:
The diameter of the circle, whose centre lies on the line $x+y=2$ in the first quadrant and which touches both the lines $x=3$ and $y=2$, is_______.
Solution:
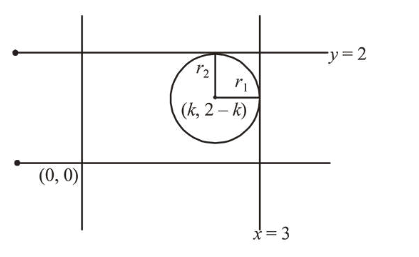
$\Rightarrow$ Radius $\left(r_{1}\right)=3-k$
$\because$ Centre lies on $x+y=2$
Let $x=k$
$\therefore y=2-k$
$\Rightarrow$ Centre $=(k, 2-k)$
Also, radius $\left(r_{2}\right)=2-(2-k)$
$\therefore 3-k=2-(2-k)$
$\Rightarrow k=\frac{3}{2}$
$r=3-\frac{3}{2}=\frac{3}{2}$
Hence, diameter $=3$.
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
