The foot of a ladder is 6 m away from a wall and its top reaches a window 8 m above the ground.

The given information can be represented as follows.

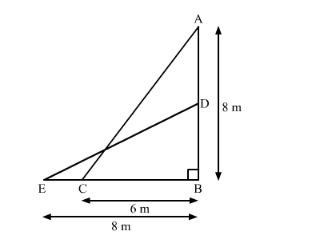
Here, A is the position of the window and AC is the ladder.

Also, DE is the same ladder when it is shifted.

C and E are the original and final position of the foot of the ladder.

Now, applying Pythagoras theorem in ΔABC,

AC2 = AB2 + BC2

⇒ AC2 = (8 m)2 + (6 m)2 = (10 m)2

⇒ AC = 10 m

Now, again applying Pythagoras theorem in ΔEBD

DE2 = EB2 + BD2

⇒ (10 m)2 = (8 m)2 + BD2

⇒ BD2 = 100 m2 − 64 m2 = 36 m2

⇒ BD = 6 m

Thus, the tip of the ladder is now at the height of 6 m above the ground.