The linear equation 3x − 5y = has

(c) infinitely many solutions

Given linear equation: $3 x-5 y=15$

Or, $x=\frac{5 y+15}{3}$

When $y=0, x=\frac{15}{3}=5$.

When $y=3, x=\frac{30}{3}=10$.

When $y=-3, x=\frac{0}{3}=0$

Thus, we have the following table:

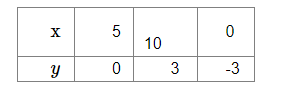
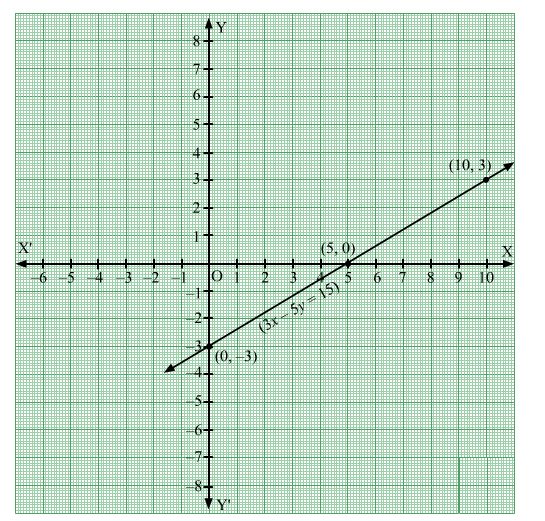
Plot the points $A(5,0), B(10,3)$ and $C(0,-3)$. Join the points and extend them in both the directions.

We get infinite points that satisfy the given equation. 
Hence, the linear equation has infinitely many solutions.