The mid-point of the sides of a triangle along with any of the vertices as the fourth point make a parallelogram of area equal to
(a) ½ ar (ABC)
(b) 1/3 ar (ABC)
(c) ¼ ar (ABC)
(d) ar (ABC)
(a) We know that, if $D, E$ and $F$ are respectively the mid-points of the sides $B C, C A$ and $A B$
of a $\triangle A B C$, then all four triangles has equal area $i . e .$,
$\operatorname{ar}(\triangle A F E)=\operatorname{ar}(\triangle B F D)=\operatorname{ar}(\triangle E D C)=\operatorname{ar}(\triangle D E F)$ $\ldots$ (i)
$\therefore$ Area of $\triangle D E F=\frac{1}{4}$ Area of $\triangle A B C$ ...(ii)
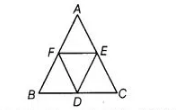
If we take $D$ as the fourth vertex, then area of the paralleiogram AFDE
$=$ Area of $\triangle A F E+$ Area of $\triangle D E F$
$=$ Area of $\triangle D E F+$ Area of $\triangle D E F=2$ Area of $\triangle D E F$ [using Eq. (i)]
$=2 \times \frac{1}{4}$ Area of $\triangle \mathrm{ABC}$ [using Eq. (ii)]
$=\frac{1}{2}$. Area of $\triangle A B C$