The midpoints of the sides BC, CA and AB of a ΔABC are D(3, 4), E(8, 9) and F(6, 7) respectively.

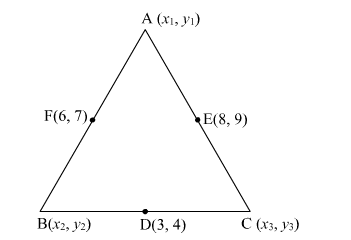
Let the coordinates of A, B, C be $\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right)$ and $\left(x_{3}, y_{3}\right)$ respectively.

Because D is the mid-point of BC, using mid-point formula, we have

$\frac{x_{2}+x_{3}}{2}=3 \quad$ and $\quad \frac{y_{2}+y_{3}}{2}=4$

$\Rightarrow x_{2}+x_{3}=6 \quad$ and $\quad y_{2}+y_{3}=8 \quad \ldots$ (i)

Similarly, E is the mid point of AC. Using mid-point formula, we have;

$\frac{\frac{x_{1}+x_{3}}{2}}{2}=8 \quad$ and $\quad \frac{y_{1}+y_{3}}{2}=9$

$\Rightarrow x_{1}+x_{3}=16 \quad$ and $\quad y_{1}+y_{3}=18 \quad \ldots$. (ii)

Again, F is the mid point of AB. Using mid point formula, we have

$\frac{x_{1}+x_{2}}{2}=6 \quad$ and $\quad \frac{y_{1}+y_{2}}{2}=7$

$\Rightarrow x_{1}+x_{2}=12 \quad$ and $\quad y_{1}+y_{2}=14 \quad \ldots \ldots$ (iii)

Adding (i), (ii) and (iii), we get

$2\left(x_{1}+x_{2}+x_{3}\right)=34 \quad$ and $\quad 2\left(y_{1}+y_{2}+y_{3}\right)=40$

$\Rightarrow x_{1}+x_{2}+x_{3}=17 \quad$ and $\quad \mathrm{y}_{1}+\mathrm{y}_{2}+\mathrm{y}_{3}=20 \quad \ldots$ (iv)

On solving equation (iv), using equations (i), (ii) and (iii), we get

$x_{1}=11$

$x_{2}=1$

$x_{3}=5$

Similarly,

$y_{1}=12$

$y_{2}=2$

$y_{3}=6$

Hence, the points are: A(11,12), B(1,2) and C(5,6).