Two concentric circles are of radii 6.5 cm and 2.5 cm.

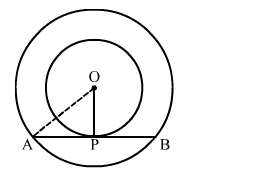
We know that the radius and tangent are perperpendular at their point of contact
In right  triangle AOP
AO2 = OP2 + PA2
⇒ (6.5)2 = (2.5)2 + PA2
⇒ PA2 = 36
⇒ PA = 6 cm
Since, the perpendicular drawn from the centre bisect the chord.
∴ PA = PB = 6 cm
Now, AB = AP + PB = 6 + 6 = 12 cm
Hence, the length of the chord of the larger circle is 12 cm.