Question.
Two congruent circles intersect each other at points A and B. Through A any line segment PAQ is drawn so that P, Q lie on the two circles. Prove that BP = BQ.
Solution:
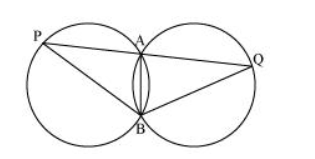
$\mathrm{AB}$ is the common chord in both the congruent circles.
$\therefore \angle \mathrm{APB}=\angle \mathrm{AQB}$
In $\triangle B P Q$,
$\angle \mathrm{APB}=\angle \mathrm{AQB}$
$\therefore B Q=B P$ (Angles opposite to equal sides of a triangle)

$\mathrm{AB}$ is the common chord in both the congruent circles.
$\therefore \angle \mathrm{APB}=\angle \mathrm{AQB}$
In $\triangle B P Q$,
$\angle \mathrm{APB}=\angle \mathrm{AQB}$
$\therefore B Q=B P$ (Angles opposite to equal sides of a triangle)
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
