Question:
Two tangents are drawn from the point $\mathrm{P}(-1,1)$ to the circle $x^{2}+y^{2}-2 x-6 y+6=0$. If these tangents touch the circle at points $A$ and $B$, and if $D$ is a point on the circle such that length of the segments $\mathrm{AB}$ and $\mathrm{AD}$ are equal, then the area of the triangle ABD is equal to:
Correct Option: , 3
Solution:
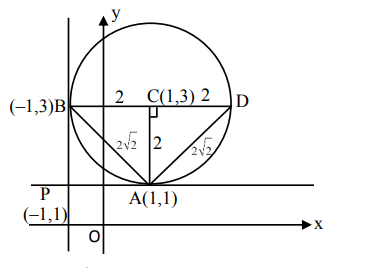
$\triangle \mathrm{ABD}=\frac{1}{2} \times 2 \times 4$
$=4$
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
