Question:
Use $\mathrm{R}=8.3 \mathrm{~J} / \mathrm{mol}-\mathrm{K}$ wherever required.
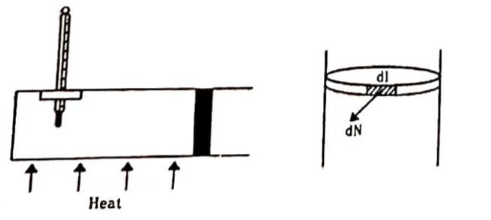
Figure shows a cylindrical tube of radius $5 \mathrm{~cm}$ and length $20 \mathrm{~cm}$. It is closed by a tight-fitting cork. The friction co-efficient between the cork and the tube is $0.20$. The tube contains an ideal gas at a pressure of $1 \mathrm{~atm}$ and a temperature of $300 \mathrm{~K}$. The tube is slowly heated and it is found that the cork pops out when the temperature reaches $600 \mathrm{~K}$. Let $\mathrm{dN}$ denote the magnitude of the normal contact force exerted by a small length dl of the cork along the periphery (see the figure). Assuming that the temperature of the gas
is uniform at any instant, calculate $\frac{d N}{d l}$
Solution:
