Verify that the numbers given along side of the cubic polynomials below are their zeros.

Solution:

We have,

$f(x)=2 x^{3}+2 x^{2}-5 x+2$

$f\left(\frac{1}{2}\right)=2\left(\frac{1}{2}\right)^{3}+\left(\frac{1}{2}\right)^{2}-5\left(\frac{1}{2}\right)+2$

$f\left(\frac{1}{2}\right)=\frac{1}{4}+\frac{1}{4}-\frac{5}{2}+2$

$f\left(\frac{1}{2}\right)=0$

$f(1)=2(1)^{3}+(1)^{2}-5(1)+2$

 

$f(1)=2+1-5+2$

$f(1)=0$

$f(-2)=2(-2)^{3}+(-2)^{2}-5(-2)+2$

$f(-2)=-16+4+10+2$

 

$f(-2)=0$

So, $\frac{1}{2}, 1$ and 2 are the zeros of polynomial $p(x)$

Let $\alpha=\frac{1}{2}, \beta=1$ and $\gamma=-2$. Then

$\alpha+\beta+\gamma=\frac{1}{2}+1-2$

$=\frac{1}{2}+\frac{1 \times 2}{1 \times 2}-\frac{2 \times 2}{1 \times 2}$

$=\frac{1+2-4}{2}$

$=\frac{-1}{2}$

From $f(x)=2 x^{3}+2 x^{2}-5 x+2$

$\alpha+\beta+\gamma=\frac{-\text { Coefficient of } x^{2}}{\text { Coefficient of } x^{3}}$

$\alpha+\beta+\gamma=-\left(\frac{1}{2}\right)$

$\alpha \beta+\beta \gamma+\gamma \alpha=\frac{1}{2}(1)+1(-2)-2\left(\frac{1}{2}\right)$

$=\frac{1}{2}-2-\frac{2}{2}$

Taking least common factor we get,

$\alpha \beta+\beta \gamma+\gamma \alpha=\frac{1}{2}-\frac{2 \times 2}{1 \times 2}-\frac{2}{2}$

 

$\alpha \beta+\beta \gamma+\gamma \alpha=\frac{1-4-2}{2}$

$\alpha \beta+\beta \gamma+\gamma \alpha=\frac{1-6}{2}$

 

$\alpha \beta+\beta \gamma+\gamma \alpha=\frac{-5}{2}$

From $f(x)=2 x^{3}+2 x^{2}-5 x+2$

$\alpha \beta+\beta \gamma+\gamma \alpha=\frac{\text { Coefficient of } x}{\text { Coefficient of } x^{3}}$

$\alpha \beta+\beta \gamma+\gamma \alpha=\frac{-5}{2}$

$\alpha \beta \gamma=\frac{1}{2} \times 1 \times(-2)$

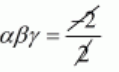
$\alpha \beta \gamma=-1$

From $f(x)=2 x^{3}+2 x^{2}-5 x+2$

$\alpha \beta \gamma=\frac{-\text { Constant term }}{\text { Coefficient of } x^{2}}$

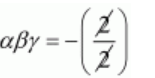
$\alpha \beta \gamma=-1$

Hence, it is verified that the numbers given along side of the cubic polynomials are their zeros and also verified the relationship between the zeros and coefficients

(ii) We have, 

$g(x)=x^{3}-4 x^{2}+5 x-2$

 

$g(2)=(2)^{3}-4(2)^{2}+5(2)-2$

$g(2)=8-16+10-2$

 

$g(2)=0$

$g(1)=(1)^{3}-4(1)^{2}+5(1)-2$

$=1-4+5-2$

 

$=0$

$g(1)=(1)^{3}-4(1)^{2}+5(1)-2$

$=1-4+5-2$

 

$=0$

So 2,1 and 1 are the zeros of the polynomial $g(x)$

Let $\alpha=2, \beta=1$ and $\lambda=1$. Then,

$\alpha+\beta+\gamma=2+1+1$

 

$\alpha+\beta+\gamma=4$

From $g(x)=x^{3}-4 x^{2}+5 x-2$

$\alpha+\beta+\gamma=\frac{\text { Coefficient of } x^{2}}{\text { Coefficient of } x^{3}}$

$\alpha+\beta+\gamma=\frac{4}{1}$

 

$\alpha+\beta+\gamma=4$

$\alpha \beta+\beta \gamma+\gamma \alpha=2(1)+1(1)+1(2)$

$\alpha \beta+\beta \gamma+\gamma \alpha=2+1+2$

 

$\alpha \beta+\beta \gamma+\gamma \alpha=5$

From $g(x)=x^{3}-4 x^{2}+5 x-2$

$\alpha \beta+\beta \gamma+\gamma \alpha=\frac{\text { Coefficient of } x}{\text { Coefficient of } x^{3}}$

$\alpha \beta+\beta \gamma+\gamma \alpha=\frac{5}{1}$

 

$\alpha \beta+\beta \gamma+\gamma \alpha=5$

$\alpha \beta \gamma=2 \times 1 \times 1$

 

$\alpha \beta \gamma=2$

From $g(x)=x^{3}-4 x^{2}+5 x-2$

$\alpha \beta \gamma=\frac{-\text { Constant term }}{\text { Coefficient of } x^{2}}$

$\alpha \beta \gamma=-\left(\frac{-2}{1}\right)$

$\alpha \beta \gamma=2$

Hence, it is verified that the numbers given along side of the cubic polynomials are their

zeros and also verified the relationship between the zeros and coefficients.