Which of the following can not be valid assignment of probabilities for outcomes of sample space

Solution:

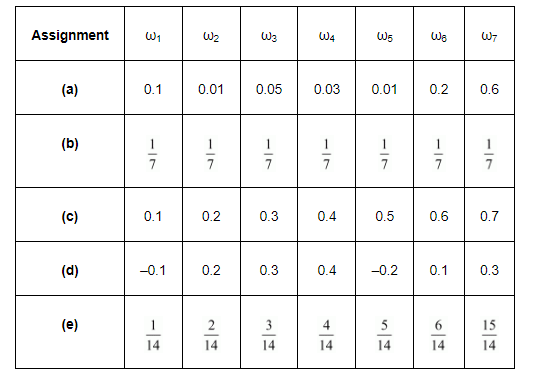
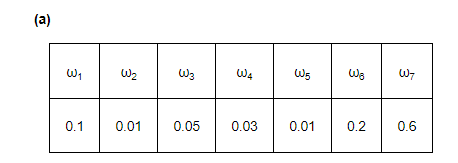
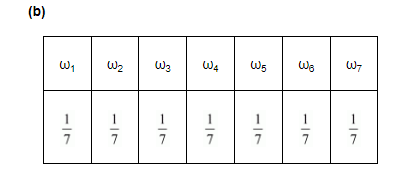
Here, each of the numbers p(ωi) is positive and less than 1.

Sum of probabilities

$=p\left(\omega_{1}\right)+p\left(\omega_{2}\right)+p\left(\omega_{3}\right)+p\left(\omega_{4}\right)+p\left(\omega_{5}\right)+p\left(\omega_{6}\right)+p\left(\omega_{7}\right)$

$=0.1+0.01+0.05+0.03+0.01+0.2+0.6$

$=1$

Thus, the assignment is valid.

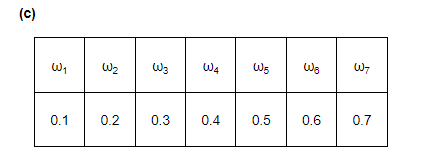
Here, each of the numbers p(ωi) is positive and less than 1.

Sum of probabilities

$=p\left(\omega_{1}\right)+p\left(\omega_{2}\right)+p\left(\omega_{3}\right)+p\left(\omega_{4}\right)+p\left(\omega_{5}\right)+p\left(\omega_{6}\right)+p\left(\omega_{7}\right)$

$=\frac{1}{7}+\frac{1}{7}+\frac{1}{7}+\frac{1}{7}+\frac{1}{7}+\frac{1}{7}+\frac{1}{7}=7 \times \frac{1}{7}=1$

Thus, the assignment is valid.

\

Here, each of the numbers p(ωi) is positive and less than 1.

Sum of probabilities

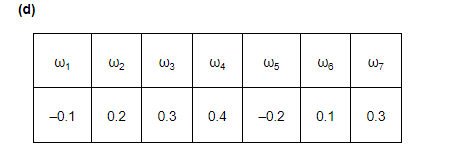
Here, $p\left(\omega_{1}\right)$ and $p\left(\omega_{5}\right)$ are negative.

Hence, the assignment is not valid.

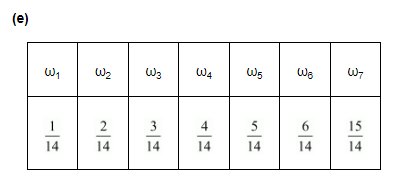
Here, $p\left(\omega_{7}\right)=\frac{15}{14}>1$

Hence, the assignment is not valid.