Write the following sets in roster form:
(i) $A=\{x: x$ is an integer and $-3 (ii) $\mathrm{B}=\{x: x$ is a natural number less than 6$\}$. (iii) $C=\{x: x$ is a two-digit natural number such that the sum of its digits is 8$\}$ (iv) $D=\{x: x$ is a prime number which is divisor of 60$\}$. (v) $E=$ The set of all letters in the word TRIGONOMETRY. (vi) $F=$ The set of all letters in the word BETTER.
(i) $A=\{x: x$ is an integer and $-3 The elements of this set are $-2,-1,0,1,2,3,4,5$, and 6 only. Therefore, the given set can be written in roster form as $A=\{-2,-1,0,1,2,3,4,5,6\}$ (ii) $B=\{x: x$ is a natural number less than 6$\}$ The elements of this set are $1,2,3,4$, and 5 only. Therefore, the given set can be written in roster form as $B=\{1,2,3,4,5\}$ (iii) $\mathrm{C}=\{x: x$ is a two-digit natural number such that the sum of its digits is 8$\}$ The elements of this set are $17,26,35,44,53,62,71$, and 80 only. Therefore, this set can be written in roster form as $C=\{17,26,35,44,53,62,71,80\}$ (iv) $D=\{x: x$ is a prime number which is a divisor of 60$\}$ $\therefore 60=2 \times 2 \times 3 \times 5$ The elements of this set are 2, 3, and 5 only. Therefore, this set can be written in roster form as D = {2, 3, 5}. (v) E = The set of all letters in the word TRIGONOMETRY There are 12 letters in the word TRIGONOMETRY, out of which letters T, R, and O are repeated. Therefore, this set can be written in roster form as E = {T, R, I, G, O, N, M, E, Y} (vi) F = The set of all letters in the word BETTER There are 6 letters in the word BETTER, out of which letters E and T are repeated. Therefore, this set can be written in roster form as F = {B, E, T, R} 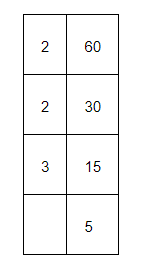
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
