A container shaped like a right circular cylinder having diameter 12 cm and height 15 cm is full of ice-cream.

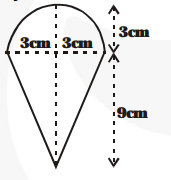
Volume of one ice-cream cone as shown in figure.

$=\frac{\mathbf{1}}{\mathbf{3}} \pi \times(3)^{2} \times 9+\frac{\mathbf{2}}{\mathbf{3}} \pi \times(3)^{3} \mathrm{~cm}^{3}$

$=27 \pi+18 \pi=45 \pi \mathrm{cm}^{3}$

volume of the ice-cream in the cylindrical container (of height $15 \mathrm{~cm}$ and diameter

$12 \mathrm{~cm})=\pi \times(6)^{2} \times 15$

Let the number of cones made be n.

Then, $n \times 45 \pi=\pi \times(6)^{2} \times 15$

$\Rightarrow 45 \mathrm{n}=36 \times 15 \Rightarrow \mathrm{n}=12$