A design is made on a rectangular

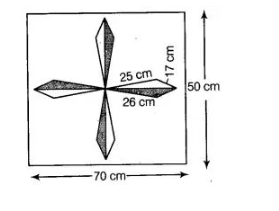
Given, the dimension of rectangular tile is $50 \mathrm{~cm} \times 70 \mathrm{~cm}$. $\therefore$ Area of rectangular tile $=50 \times 70=3500 \mathrm{~cm}^{2}$

The sides of a design of one triangle be

$a=25 \mathrm{~cm}, b=17 \mathrm{~cm}$ and $c=26 \mathrm{~cm}$

Now, semi-perimeter, $s=\frac{a+b+c}{2}=\frac{25+17+26}{2}=\frac{68}{2}=34$

$\therefore \quad$ Area of one triangle $=\sqrt{s(s-a)(s-b)(s-c)}$ [by Heron's formula]

$=\sqrt{34 \times 9 \times 17 \times 8}$

$=\sqrt{17 \times 2 \times 3 \times 3 \times 17 \times 2 \times 2 \times 2}$

$=17 \times 3 \times 2 \times 2=204 \mathrm{~cm}^{2}$

$\therefore$ Total area of eight triangles $=204 \times 8=1632 \mathrm{~cm}^{2}$

Now, area of the design $=$ Total area of eight triangles

$=3500-1632$

$=1868 \mathrm{~cm}^{2}$

Hence, the total area of the design is $1632 \mathrm{~cm}^{2}$ and the remaining area of the tile is $1868 \mathrm{~cm}^{2}$.