AD is an altitude of an equilateral triangle ABC. On AD as base,

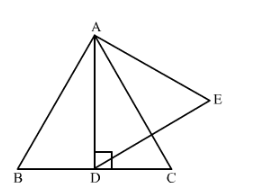
We have an equilateral triangle $\triangle A B C$ in which $\mathrm{AD}$ is altitude. An equilateral triangle $\triangle A D E$ is drawn using $\mathrm{AD}$ as base. We have to prove that, $\frac{a r(\Delta A D E)}{a r(\Delta A B C)}=\frac{3}{4}$

Since the two triangles are equilateral, the two triangles will be similar also.

$\triangle A D E-\triangle A B C$

We know that according to the theorem, the ratio of areas of two similar triangles is equal to the ratio of the squares of any two corresponding sides.

$\frac{\operatorname{ar}(\Delta A D E)}{\operatorname{ar}(\Delta A B C)}=\left(\frac{A D}{A B}\right)^{2}$....(1)

Now $\triangle A B C$ is an equilateral triangle. So,

$\angle B=60^{\circ}$

Therefore,

$\sin \angle B=\frac{A D}{A B}$

So, $\frac{A D}{A B}=\frac{\sqrt{3}}{2}$

We will now use this in equation (1). So,

$\frac{\operatorname{ar}(\Delta A D E)}{\operatorname{ar}(\Delta A B C)}=\left(\frac{A D}{A B}\right)^{2}$

$=\left(\frac{\sqrt{3}}{2}\right)^{2}$

$=\frac{3}{4}$

Hence, proved.