Express each of the following decimals in the form $\frac{p}{q}$ :
(i) $0.39$
(ii) $0.750$
(iii) $2.15$
(iv) $7.010$
(v) $9.90$
(vi) $1.0001$
(i) Given decimal is $0.39$
Now we have to convert given decimal number into the $\frac{p}{q}$ form
Let $\frac{p}{q}=0.39$
$\Rightarrow \frac{p}{q}=\frac{39}{100}$
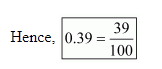
(ii) Given decimal is $0.750$
Now we have to convert given decimal number into $\frac{p}{q}$ form
Let $\frac{p}{q}=0.750$
$\Rightarrow \frac{p}{q}=\frac{750}{1000}$
$\Rightarrow \frac{p}{q}=\frac{75}{100}$
$\Rightarrow \frac{p}{q}=\frac{3}{4}$
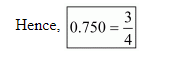
(iii) Given decimal is $2.15$
Now we have to express the given decimal number into $\frac{p}{q}$ form
Let $\frac{p}{q}=2.15$
$\Rightarrow \frac{p}{q}=\frac{215}{100}$
$\Rightarrow \frac{p}{q}=\frac{43}{20}$
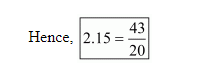
(iv) Given decimal is $7.010$
Now we have to express the given decimal number into $\frac{p}{q}$ form
Let $\frac{p}{q}=7.010$
$\Rightarrow \frac{p}{q}=\frac{7010}{1000}$
$\Rightarrow \frac{p}{q}=\frac{701}{100}$
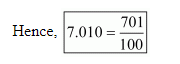
(v) Given decimal is $9.90$
Now we have to find given decimal number into $\frac{p}{q}$ form
Let $\frac{p}{q}=9.90$
$\Rightarrow \frac{p}{q}=\frac{990}{100}$
$\Rightarrow \frac{p}{q}=\frac{99}{10}$
Hence, $9.90=\frac{99}{10}$
(vi) Given decimal is $1.0001$
Now we have to find given decimal number into $\frac{p}{q}$ form
$\frac{p}{q}=1.0001 \Rightarrow \frac{p}{q}=\frac{10001}{10000}$
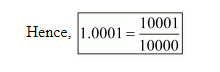
Click here to get exam-ready with eSaral
For making your preparation journey smoother of JEE, NEET and Class 8 to 10, grab our app now.
