Question:
(i)Find the number of different words by using all the letters of the word, ‘INSTITUTION’. In how many of them
(ii) are the three T's together
(iii) are the first two letters the two $\mathbf{N}^{\prime} \mathbf{s}$ ?
Solution:
(i) There are 11 letters of which 3 are of 1 kind, 2 are of the 2nd kind ,3 are of the 3rd kind
Number of arrangements $=\frac{11 !}{3 ! 2 ! 3 !}=554400$
(ii) Let all the three T's be denoted by a single letter Z
New word is INSIUIONZ
Number of permutations $=\frac{9 !}{3 ! 2 !}=30240$
(iii)
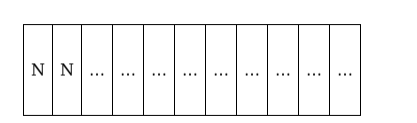
There are 9 places to be filled by 9 letters of which 3 are of 2 different kinds
Number of permutations $=\frac{9 !}{3 ! 3 !}=10080$